Letterblock Diceware Passwords
I wanted to give my son a diceware list and realized that giving him a printout of 5 pages in fine print would just not work out.
Diceware passwords use wordlists, but those are hard to type, because they have lots of letters. I’ve been using Letterblock passwords as shorter alternative for a while, but wanted a version that works offline. This is it.1
This form includes validation and automatically fixes common reading errors (like =O= instead of =0= or =G= instead of =6=). To use it for password input, change the input type from =text= to =password= and the validate button type to =submit=.
Aaron Toponce contributed many improvements to the javascript implementation (via his gist). Thank you!
To use Letterblock Diceware Passwords offline with dice, print business-cards with the following template. Deepest thank you goes to Karol Kozioł who allowed me to use the business-card template under free licenses (see letterblock-diceware-card.tex for details).
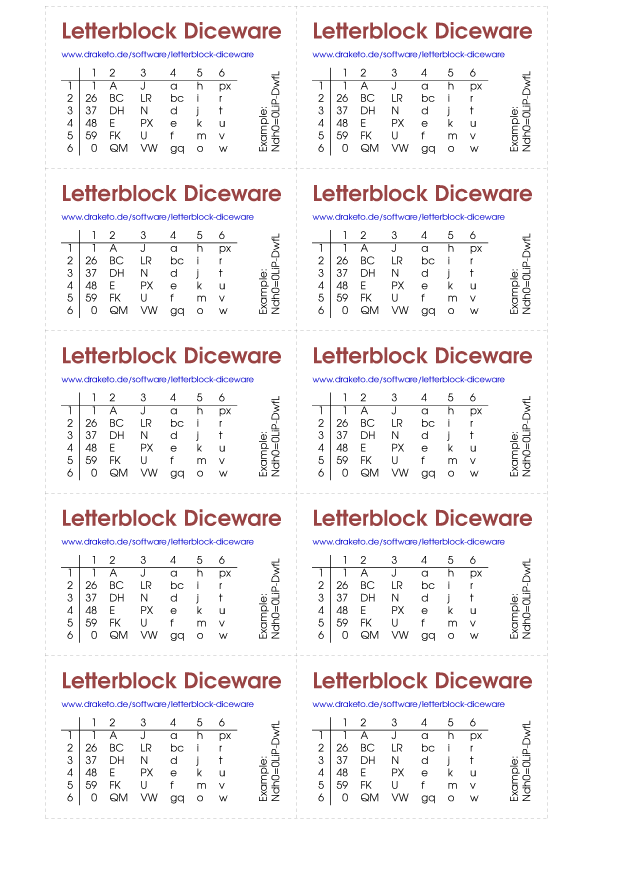
Create a letterblock diceware password
Roll two dice per letter. If the result has multiple letters, choose the one which makes the password easiest to pronounce.
Roll up at least two blocks of four letters each. Each block has slightly more than 20 bits of entropy.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 1 | A | J | a | h | px |
| 2 | 26 | BC | LR | bc | i | r |
| 3 | 37 | DH | N | d | j | t |
| 4 | 48 | E | PX | e | k | u |
| 5 | 59 | FK | U | f | m | v |
| 6 | 0 | QM | VW | gq | o | w |
After rolling the blocks, add the row-numbers (vertical) of the results of two consecutive blocks, take modulo 6, and choose from the following list:
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| . | + | - | = | @ | % |
Example with 2 blocks, entropy 40: Niru=13J5
| rolled: | 33 | 52 | 62 | 64 |
|---|---|---|---|---|
| letters: | N | i | r | u |
| rolled: | 11 | 13 | 31 | 15 |
|---|---|---|---|---|
| letters: | 1 | 37 | J | 59 |
Separator: Add rows: 3+2+2+4+1+3+1+5 = 21, modulo 6 = 3 ⇒ =.
Background
This is an evolution of the older Letterblock passwords which use 55 letters that are unambiguous in handwriting and safe to use in URLs, grouped in blocks of four letters to make them easier to remember, with separators that work as weak checksum to catch many typing errors before even sending the password to the server, with weak optimization for legibility by creating 8 passwords and choosing the one with bigrams that are closest to regular prose.
This letterblock diceware uses 51 letters that are unambiguous to write by hand. Compared to regular letterblocks, n and G were removed, because unclean n often looks like a u and unclean G looks like 6, and s was removed because it often looks like 5:
define base51 "0123456789ABCDEFHJKLMNPQRTUVWXabcdefghijkmopqrtuvwx"
As delimiters it only uses symbols that are available on every keyboard and are safe to use in most contexts:
define base51-delimiters ".+-=@%"
To recover from common reading errors, use the following lookup table:
define base51-correct-reading-errors ' ; e . c: e = error, c = corrected G . 6 I . 1 O . 0 S . 5 Y . X Z . 2 l . 1 n . u s . 5 y . x z . 2
The letters ordered by the probability of the most common bigram in which they are second letter in prose:
define letters-by-probability
. "rheidtcguamobfkpxw0v981526437qBEjTDRANLPUWHFMCVKXQJ"
The 51 symbols are collapsed into 36 die-roll-results using four principles:
- Do not collapse vowels. They make for easier pronouncability.
- Do not collapse 1 and 0. They make for simpler compound numbers.
- Prefer collapsing uppercase letters. These are harder to type (you must hold down shift).
- Prefer collapsing rare consonants to make it less likely to hit uncommon sounds.
The entropy of these passwords is 5.17 per letter, without counting the delimiters. So you get roughly 20 bits of entropy per block. For details, see the article about the previous version (the math still applies, just with slightly changed parameters).
Comparison
A diceware password delivers 12.92 bits of entropy per word. 6 words of 3 to 6 letters provide 77 bits of entropy, while 4 blocks of a letterblock password provide 80 bits of entropy.
Diceware using the eff memorable short word list with only 4 rolls per word delivers 10.34 bits of entropy per word, so you need 8 words to have more than 80 bits of entropy. Since these words are 3-5 characters, a short diceware password will require typing roughly twice as many characters compared to a letterblock diceware password. It is easier to memorize, though (if you speak english).
I prefer letterblock diceware passwords, because I made too many typing errors with diceware.
Footnotes:
Diceware also has tables for random characters, but these do not create easy to memorize passwords.

